Computational Physics VRC
Application description
Geophysical inversion remains a difficult problem classified as ill posedwith the definition of Hadamard, where physical parameters of 3D geosection have to be evaluated on basis of values measured in a 2D surface array. Despite the progress it remains
uncertainand practical solutions of the problem yet are constrained for convex bodies, regular bodies, or simplified 2D problems
Except the uncertainty of extrapolation of information from a 2D array into a 3D geosection, the complication of 3D case is conditioned by the huge volume of data representing 3D structures. In a geosection extended for kilometers different geological objects may have thin shapes of the size of one meter or less, which implies in the general case the need for a multitude of O(10^9) discretization nodes. Volume of data implies huge calculation power necessary for their processing, and this is another obstacle for fast calculations required when interactive applications are used.
Application's goal
The use of grid and parallel systems for fast calculations may help engineers to apply simple algorithms for complicated problems, balancing the complexity with the calculation power of such platforms. In this context it is proposed an application for the 3D geophysical inversion of gravity anomalies, using a simple calculation methodology, and its timing performances when executed in a parallel were evaluated. Gravity field was selected as being the simplest case in the complex of geophysical methods (magnetism and electricity), allowing to focus on computational issues.
How the goal is reached
The work was based on the the traditional formula for the vertical gradient of gravitational potential field used in geophysical surveys. The 3D geosection is discretized in elementary cuboids with mass concentrated in respective centers. Iteratively the density mass of a single cuboid is updated, cuboid selected such that its ground surface effect gives the best match for the observed anomaly. In the figure a schematic view of the discretized geosection under the observed surface anomaly of vertical gravity gradient is presented.
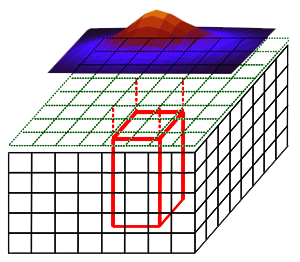
Fig. - geosection model (- ~ 3D geosection array; ? ~
2D surface profiles array; ? ~ anomalous body)
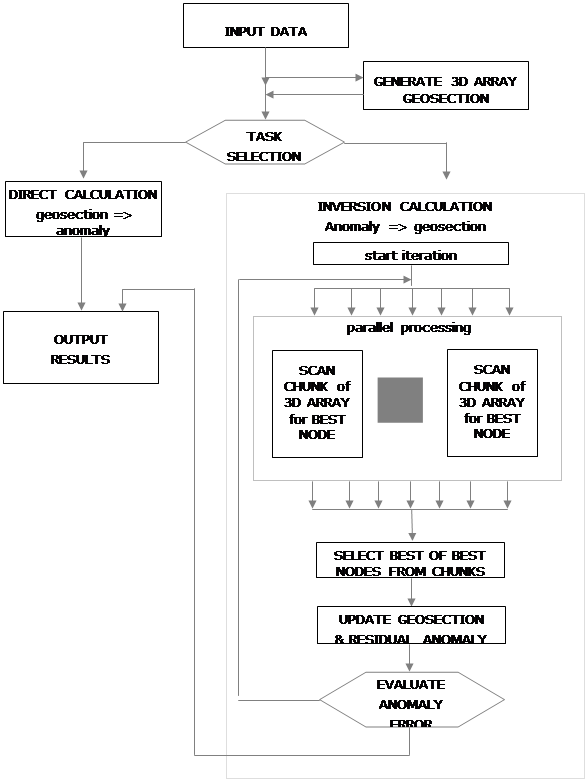
The inversion is realized using the idea behind the algorithm CLEAN of Högbom using an iterative process as follows:
- starting with a 3D geosection array representing the rocks density and initialized by zeros, and a 2D gravity anomaly array measured in the field
- searching the node in the geosection array, which effect offers the best least square approximation of the gravity anomaly array
- incrementing the density of the selected node by a fixed amount (density step)
- subtracting the effect of the modification of the geosection from the surface gravity anomaly
- repeating the steps (b):(c):(d) until residual anomaly changes less than a fixed predefined value.
Modules/components
The application has four principal components:
- input module
- direct calculation of gravity anomaly
- inversion of gravity anomaly
- output modul
The input module can generate synthetic geosections composed by several vertical prisms defined by coordinates of their extremal corners, allowing the user to generate anomalies for know geological structures or models, using the direct calculation module. Typically the application can be used in several scenarios:
first scenario: generation of anomalies created by several prisms,
second scenario: generation of anomalies for complex geosections
third scenario: inversion of given anomalies producing geosections
The tests carried out in framework of the project were combination of first scenario (generation of anomalies from one or two prisms), and third scenario (inversion of these anomalies using different parallelization levels).
Runtime and approximation of inverted solutions were used for the evaluation of qualities of the application.
Programming techniques (in brief)
Parallelization is done using two technologies: OpenMP and MPI. Within the iteration the loop scanning the 3D geosection while searching the best node is parallelized splitting the 3D array of nodes in chunks (dotted rectangle in the flowchart).
User guide
Both input and output consist in single text files.
Input file contains model parameters and one of:
prismatic coordinates (first scenario), or
3D geosection array of mass density for each cuboid (second scenario), or
2D surface anomaly array for inversion (third scenario)
Output file contains:
model parameters (the same as input)
2D array of surface anomaly (generated or inverted)
3D geosection array (whole or single 2D section)
Input/output
|
|
Values of 2D array are in order [X][Y].
Values of 3D array are in order [X][Z][Y].
User operations
Execution of the program depends on parallelization method:
execution for OpenMP:- <GIM executable> <input file> <output file> <error file> NoProc=<T>
- where: <T> ~ number of parallel threadsexecution for MPI:
- mpirun -np <P> <GIM executable> <input file> <output file> <error file>
- where: <P> ~ number of parallel processes.User can configure the application through these parameters:
| Pout | ~ defines printing of whole 3D array or a single YZ plane |
| TopOw | ~ defines the error mode for selection of best 2D node simple least squares error within a window defined by Wfac weighted least squares error, using the amplitude of the node's gravity effect as weight |
| Wfac ~ | defines the size of simple least squares error window relative to the curvature of the node's gravity effect |
ErMo |
~ defines the criteria for termiantion of iterations: the average of absolute values of residual anomaly less than predefined limit, or when the update calculated for the best 3D node results less than half of mass density step. |
Available user support
User support is available via email <nfrasheri@fti.edu.al>
Scientific results
Inversion of gravity anomaly for the single body model gave good delineation of the body as shown in the figure:
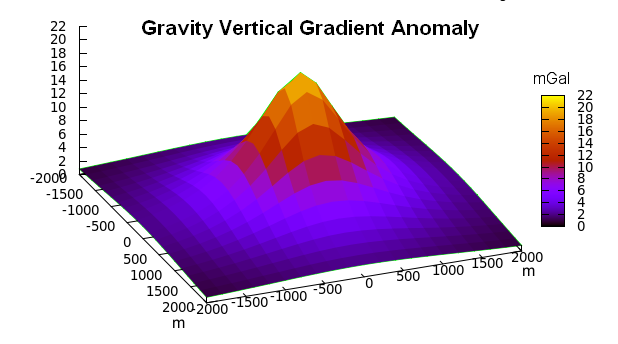
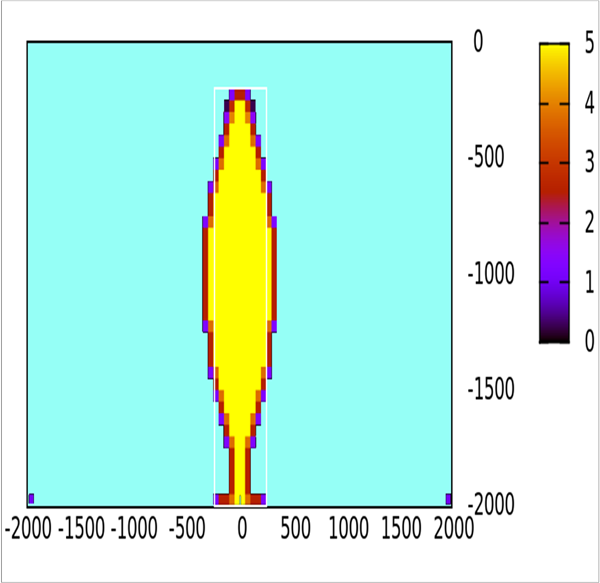
The mass density contrast in the inverted geosection matches the physical reality. The shape of the inverted body resulted rounded, expression of being an ill-posed problem. OpenMP runtime for the single body model in SGE is presented in Fig. 4.
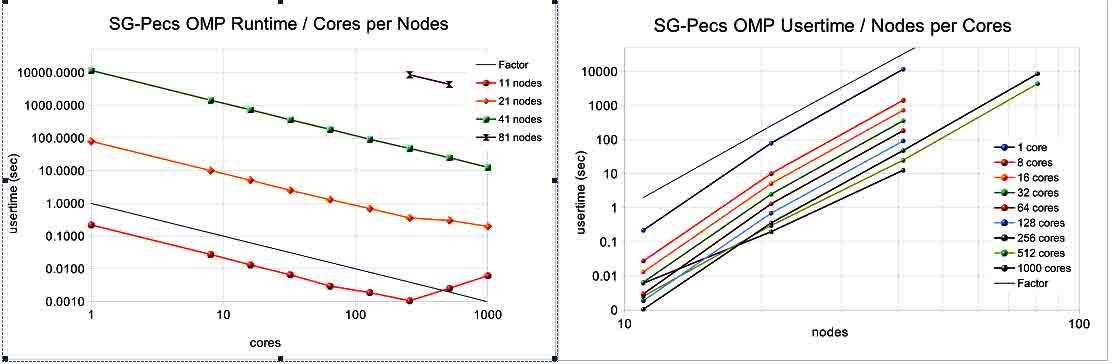
Runtime decreased with the increase of the number of cores following the predicted rate described as O(1/cores). The increase of runtime with the increase of the model size (expressed with the number of linear 3D nodes in one edge of the geosection) followed the expected rate described as O(N8). The scalability resulted “spoiled” in cases of small models run in many parallel cores, resulting from the overhead in swapping of multitude of “small” threads. Similar results were obtained for HPCG, without reaching the situation of “spoiled” runtime for small models because the number of threads was limited. MPI runtime for the single body model in HPCG is presented in Figure:
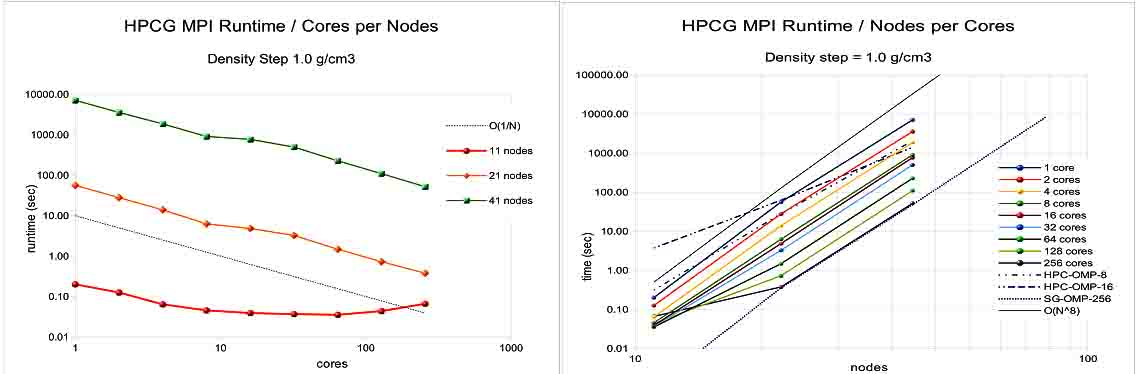
The scalability with MPI resulted similar with the OpenMP, presenting the same order: O(1/cores) decrease with number of cores and and O(N8) increase with the model size. For small models MPI resulted more sensible to the number of cores, the runtime “spoiled” very fast when the number of cores increased.
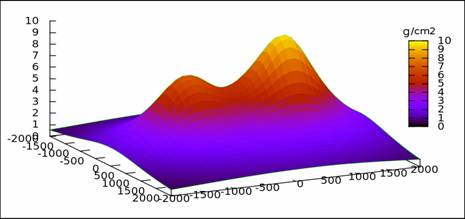
The algorithm gave relatively good results for the inversion of a single prismatic body. In order to evaluate its performances in real situations a two-body model was experimented, with the gravity anomaly presented in Figure:
Despite the fact that this anomaly is created by two bodies, it may be considered as created by a deep body and two shallow ones. The inverted geosection resulted as in Figure:
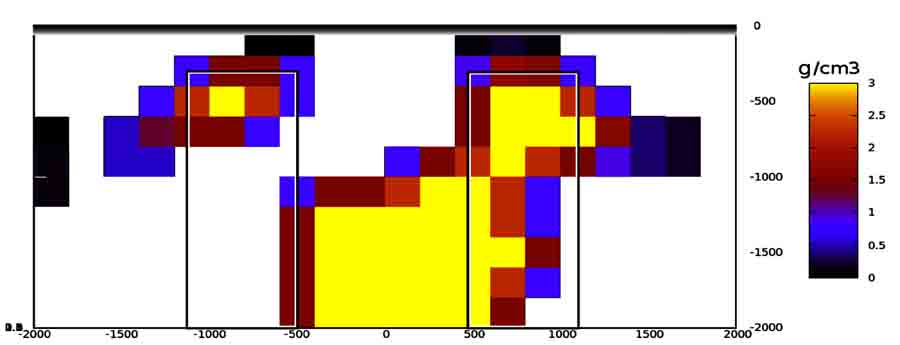
The inverted geosection resulted as composed by two parts. The shallow part includes two bodies situated in the right place (over original bodies), while the second part in depth has only one body situated between original ones like a "bridge", a phenomenon found in the literature as well.
Scientific publications
The presentations in project's training and dissemination events in Tirana are not included in publications list hereunder.
Papers from User Forum in Belgrade 2012 and ICTI'2012 are in review process for publication in Springer Series, and not included in publications list hereunder.
Papers
- N. Frasheri, S. Bushati. An Algorithm for Gravity Anomaly Inversion in HPC. SCPE: Scalable Computing: Practice and Experience vol. 13 no. 2, pp. 51-60 (http://www.scpe.org/index.php/scpe).
- N. Frasheri, B. Cico. Analysis of the Convergence of Iterative Geophysical Inversion in Parallel Systems. Springer Advances in Intelligent and Soft Computing 150: ICT Innovations 2011 (ed. L. Kocarev). Springer-Verlag 2012
Proceedings
- N. Frasheri, B. Cico. Reflections on parallelization of Gravity Inversion. HP-SEE User Forum, 17-19 October 2012, Belgrade, Serbia.
- N. Frasheri, B. Cico. Scalability of geophysical Inversion with OpenMP and MPI in Parallel Processing. ICT Innovations 2012. 12 - 15 September, Ohrid, Macedonia.
- N. Frasheri, B. Cico. Convergence of gravity inversion using OpenMP. XVII Scientific-Professional Information Technology Conference 2012, 27 February - 2 March 2012, Žabljak Montenegro
- N. Frasheri, S. Bushati. An Algorithm for Gravity Anomaly Inversion in HPC. SYNASC 2011 - 13th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, September 26-29, 2011, Timisoara, Romania
- N. Frasheri, B. Cico. Analysis of the Convergence of Iterative Gravity Inversion in Parallel Systems. ICT Innovations 2011 Conference, Macedonian Academy of Sciences and Arts (MANU), Skopje, 14-16 September 2011
Presentations
- N. Frasheri, S. Bushati, A. Frasheri. A Parallel Processing Algorithm for Gravity Inversion. Accepted in Geophysical Research Abstracts, Vol. 15, EGU2013-8739, 2013, EGU General Assembly 2013
- N. Frasheri, B. Cico. Computing developments in Albania and it's applications. International Workshop on recent LHC results and related topics. 8-9 October 2012, Tirana, Albania
- N. Frasheri. HP and High Performance Computing in Albania. HP Solutions Event, 26 Septemebr 2012, Tirana Albania

 Infrastructure for South East Europe's Research Communities
Infrastructure for South East Europe's Research Communities